[Uni Tübingen] - [Mat.-Nat. Fakultät] - [Fachbereich Chemie] - [Anorg. Chemie] - [Klaus Eichele] - [NMR Ramblings] - [Tensor Conventions] - Chemical Shift Tensors
 |
Chemical Shift Tensor ConventionsContents: [Online converter] [Chemical shift / shielding] [Chemical shift tensors] [Standard] [Herzfeld-Berger] [Haeberlen] [References] |
Online Converter between Different Conventions
Chemical Shift and Absolute Magnetic Shielding
It is recommended that the IUPAC conventions [1] are obeyed:
- The absolute magnetic shielding, σ, in ppm is the difference in
shielding between the frequency of the bare nucleus, νnucl, and the
frequency of the same nucleus in the species under investigation, νs:
σ / ppm = 106*(νnucl-νs)/νnucl
- The chemical shift, δ, is the difference in shielding between the nucleus in the species under investigation, σs, and the
shielding of the same nucleus in a reference compound, σref:
δ / ppm = 106*(σref-σs)/(1-σref) = 106*(νs-νref)/νref; approx.: 106*(σref-σs)
Because σref is often a small number compared to 1, frequently the latter approximation is used. However, one should be aware of the approximate nature of this formulation, because for nuclei with large chemical shift ranges the difference can amount up to several hundreds of ppm! Also, on some NMR instruments the transmitter frequency is used instead of the frequency of the reference compound.
N.B. For some nuclei, different reference compounds are in existence. To convert chemical shifts from one scale to the other, one should not simply add or subtract the chemical shift difference between the two reference compounds from the chemical shift of the sample. Instead, it is necessary to account for the change in the reference frequency, too [7]:
δ = δ'(Ξ'ref/Ξref) + 106(Ξ'ref-Ξref)/Ξref
- The "chemical shit" [sic] scale is another scale that can be found in the literature. There are
even patents referring to this scale! (Because the original page from PatenTrust is not available anymore, I am
mirroring the content here) Luckily, it is reasonably simple
to convert chemical shits to chemical shifts by multiplying the chemical shit by a factor of 1.
Some of the papers using this scale are:
Biochemistry 1988, 27, 5161 | Biochemistry 1996, 35, 4314 | Biochemistry 2003, 42, 13066 | Inorg. Chem. 1981, 20, 489 | Inorg. Chem. 1982, 21, 1641 | J. Am. Chem. Soc. 1991, 113, 3583 | J. Org. Chem. 2001, 66, 3775 | J. Org. Chem. 2002, 67, 5117 | Langmuir 1999, 15, 7894 | Macromolecules 1985, 18, 928 | Macromolecules 1993, 26, 3698 | Macromolecules 1999, 32, 8033 | Macromolecules 2003, 36, 667 | Organometallics 1987, 6, 777 | Organometallics 1987, 6, 788 | Org. Proc. Res. Develop. 2003, 7, 954
Recent research by W. Robien shows that even a data base of chemical shits exists. - A similar scale is the "chemical shirt" [sic] scale, discovered in the Web of Science database, also with a conversion factor of 1 (click on the image for an enlarged view):
Shifts, commonly used in solution and solid state NMR studies, are thus positive to high frequency. Absolute shieldings are positive to low frequency, and are only accessible via theoretical calculations. The establishment of a correspondence between a chemical shift scale and a magnetic shielding scale is not a trivial task and requires both careful theoretical calculations and experimental measurements [2].
The nuclear magnetic shielding (absolute shielding) is the molecular electronic property. The chemical shift is a quantity that we experimentalists have defined and use because of our inability to directly measure the absolute magnetic shielding. This inability results from our inability to know the magnitude of the magnetic field to an accuracy on the order of parts per billion, independent of the resonance experiment [3].
Comments
The symbol σ should only be used for absolute shieldings. Often, however, authors use a "pseudo" shielding scale, where the "shielding" is obtained by simply reversing the sign of the chemical shift. In our opinion, this adds only to the confusion without providing any additional insight.
Chemical Shift Tensors
Depending on the local symmetry at the nuclear site, the magnitude of the chemical shift will vary as a function of the orientation of the molecule with respect to the external magnetic field. This orientation dependence of the chemical shift is referred to as chemical shift anisotropy (CSA). Mathematically, the chemical shift anisotropy is described by a second-rank tensor (a 3 by 3 matrix), which in the case of the symmetric part of the chemical shift (CS) tensor consists of six independent components. Generally, one is able to express the chemical shift tensor in a coordinate frame where all off-diagonal elements vanish. In this principal axis system, the chemical shift tensor is fully described by the three diagonal elements - the principal components - and the three eigenvectors or Euler angles describing the orientation of the principal axes with respect to an arbitrary frame. In addition, various combinations of the principal components (and their orientations) are in use to describe the chemical shift tensor. Some of these conventions will be described in the next sections.
Standard Convention
 |
|
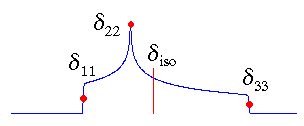
In the standard convention, the principal components of the chemical shift tensor, (δ11, δ22, δ33), are labeled according to the IUPAC rules [4]. They follow the high frequency-positive order. Thus, δ11 corresponds to the direction of least shielding, with the highest frequency, while δ33 corresponds to the direction of highest shielding, with the lowest frequency. The isotropic values, δiso, are the average values of the principal components, and correspond to the center of gravity of the line shape.
The term "standard convention" has been coined by me to distinguish it from the other conventions. Of course, other groups will call in turn their convention the standard. So far, NMR spectroscopists are still fighting about the best way to report tensors. I think that it doesn't really matter as long as people clearly state their definitions.
My programs use this convention!
Herzfeld-Berger Convention
 |
|
In the Herzfeld-Berger notation [5], a tensor is described by three parameters,
which are combinations of the principal components in the standard notation:
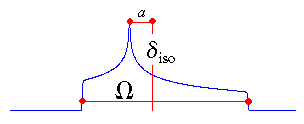
The isotropic value, i.e., the centre of gravity, is the average value of the principal components.
The span describes the maximum width of the powder pattern.
The skew of the tensor is a measure of the amount and orientation of the asymmetry of the
tensor. As indicated, κ is given by 3a/Ω.
Depending on the position of δ22 with respect to
δiso, the sign is either positive or negative. If δ22
equals δiso, a and the skew are zero. In the
case of an axially symmetric tensor, δ22 equals
either δ11 or δ33 and a = Ω/3. Hence, the skew is ±1.
The parameter μ used with the Herzfeld-Berger tables is related to the span of a tensor by:
μ = Ω*νref/spinning rate
The parameter ρ used with the Herzfeld-Berger tables corresponds to the skew of a tensor described here. The Herzfeld-Berger convention is related to the Standard convention via:
δ22 = δiso+κ Ω/3
δ33 = (3δiso-δ22-Ω)/2
δ11 = 3δiso-δ22-δ33
Note that the exact formulation of the span, Ω, contains the factor (1-σref) [3]:
Ω = (δ11-δ33)(1-σref)
Haeberlen Convention
 |
|
The Haeberlen-Mehring-Spiess convention uses different combinations of the
principal components to describe the line shape [6]. This convention
requires that the principal components are ordered according to their separation from the
isotropic value.
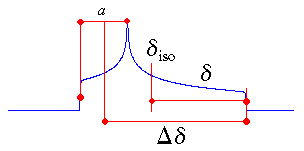
The centre of gravity of the line shape is described by the isotropic value, which is the average
value of the principal components.
The anisotropy and reduced anisotropy describe the largest separation from the centre of
gravity. (The term reduced anisotropy is not used in the literature, but I introduce it here in
order to be able to distinguish between "Haeberlen's δ" and Δδ ;
the use of the symbol δ is somewhat unfortunate, because it is more commonly used to
represent chemical shifts.) The sign of the anisotropy indicates on which side of the isotropic value one can
find the largest separation.
The asymmetry parameter indicates by how much the line shape deviates from that of an
axially symmetric tensor. In the case of an axially symmetric tensor, a =
(δyy - δxx) will be zero and hence η = 0.
Unfortunately, there are also some conventions in which the order of the components δ yy and δxx is interchanged, as well as other definitions of Δδ.
The Haeberlen-Mehring convention is related to the Standard convention via:
| for δ > 0 (i.e. δzz = δ11) | for δ < 0 (i.e. δzz = δ33) | ||
| δ11 = δiso+δ | δ33 = δiso+δ | ||
| δ22 = δiso-δ(1-η)/2 | δ22 = δiso-δ(1-η)/2 | ||
| δ33 = δiso-δ(1+η)/2 | δ11 = δiso-δ(1+η)/2 |
The program SIMPSON by M. Bak uses this convention!
References
| [1] | Pure Appl. Chem. 1972, 29, 625, DOI: 10.1351/pac197229040625 ; 1976, 45, 217, DOI: 10.1351/pac197645030217 . |
| [2] | Some examples for established shielding scales: Carbon: A. K. Jameson, C. J. Jameson, Chem. Phys. Lett. 1987, 134, 461, DOI: 10.1016/0009-2614(87)87173-7 . W. T. Raynes, R. McVay, S. J. Wright, J. Chem. Soc., Faraday Trans. 2 1989, 85, 759, DOI: 10.1039/F29898500759 . Silicon: C. J. Jameson, A. K. Jameson, Chem. Phys. Lett. 1988, 149, 300, DOI: 10.1016/0009-2614(88)85030-9 . Phosphorus: C. J. Jameson, A. De Dios, A. K. Jameson, Chem. Phys. Lett. 1990, 167, 575, DOI: 10.1016/0009-2614(90)85472-O . Tin: A. Laaksonen, R. E. Wasylishen, J. Am. Chem. Soc. 1995, 117, 392, DOI: 10.1021/ja00106a044 . |
| [3] | C. J. Jameson, Solid State Nucl. Magn. Reson. 1998, 11, 265, DOI: 10.1016/S0926-2040(98)00029-0 . |
| [4] | J. Mason, Solid State Nucl. Magn. Reson. 1993, 2, 285, DOI: 10.1016/0926-2040(93)90010-K . |
| [5] | J. Herzfeld, A. E. Berger, J. Chem. Phys. 1980, 73, 6021, DOI: 10.1063/1.440136 . |
| [6] | U. Haeberlen, In Advances in Magnetic Resonance; Suppl. 1; J. S. Waugh, Ed.; Academic Press: New York, 1976. M. Mehring, Principles of High Resolution NMR in Solids, 2nd. ed.; Springer Verlag: Berlin, 1983. H. W. Spiess, In NMR Basic Principles and Progress; P. Diehl, E. Fluck, R. Kosfeld, Eds.; Springer Verlag, Berlin, 1978, Vol. 15. |
| [7] | R. G. Kidd, R. J. Goodfellow, In NMR and the Periodic Table; R. K. Harris, B. E. Mann, Eds.; Academic Press, London, 1978. |
[ Anorg. Chemie ] | [ Go Home ] | webm@ster | last modified: 18.08.2023

