[Uni Tübingen] - [Mat.-Nat. Fakultät] - [Fachbereich Chemie] - [Anorg. Chemie] - [Klaus Eichele] - [NMR Ramblings] - Tensor Conventions

|
Tensor ConventionsContents: [Introduction] - [Chemical shift tensors] [Quadrupolar tensors] - [Euler angles] [Quick-chart WSolids / Simpson] - [References] |
Introduction
This page contains some information on specifying tensor quantities in NMR, especially chemical shift tensors and electric field gradient tensors (quadrupolar interaction), as well as comments on Euler angles. The information presented here is aimed at users of some of my programs that also use the program SIMPSON, by Mads Bak.
No area is so confusing and frustrating as the interplay of quadrupolar and chemical shift interaction. For each interaction, there are several possible conventions, and a few additional permutations in combining them. Often, it is not obvious what convention has been used in the literature. Apparent disagreements can often be traced to differences in convention. A very good review is Man's contribution to the NMR encyclopedia [1].
In order to better understand the pitfalls, I recommend to first read the information provided on chemical shift tensors, quadrupolar tensors, and Euler angles by following the links provided below.
Chemical Shift Tensors
There are quite a few different ways of describing chemical shift tensors!
Quadrupolar Tensors
The situation is not so bleak in case of quadrupolar tensors describing the interaction between an electric nuclear quadrupole moment with the electric field gradient about the nucleus.
Euler Angles
But it's bad again in the case of Euler angles that describe rotations or relative orientations of coordinate systems.
Quick-Chart WSolids / Simpson
As indicated in the sections on chemical shift tensors, quadrupolar tensors, and Euler angles, there are different possibilities to work with tensorial properties. To make matters worse, all the building blocks above can be put together in different combinations. However, on this page I will focus on some differences between WSolids or some of my other programs, and SIMPSON, the program by M. Bak.
Both programs use slightly different conventions for reporting chemical shift tensors. Thus, there are two different ways required to switch from one program to the other:
In cases where δzz of SIMPSON corresponds to
δ33 of WSolids, the principal axis systems are conincident
and there is only a difference in the way the Euler angles are used: Simpson uses the Euler angles to rotate
the PAS of the chemical shift tensor into the reference frame, while WSolids uses the Euler angles to rotate
the reference frame into the PAS of the chemical shift tensor. Given a set of Euler angles for Simpson,
{α(Simpson), β(Simpson), γ(Simpson)},
one can easily calculate the corresponding set for WSolids:
{α(WSolids), β(WSolids), γ(WSolids)} =
{-γ(Simpson), -β(Simpson), -α(Simpson)}
The situation is a little more complicated in cases where δzz of SIMPSON corresponds to δ11 of WSolids. If we simply relabel the principal axes in the WSolids convention using the Simpson convention, we interchange the meaning of the δ11 and δ33 axes and actually create a left-handed coordinate system. Therefore, I have inverted in the following quick chart the direction of δxx. The interchange of axes also means, in addition to the previous rule for Euler angle conversion, a constant additional phase shift of -90 for the Euler angle β (except for cases where in WSolids the Euler angle γ differs from 0, then the phase shift is to γ).
In the following quick chart, the first column of images lists a few canonical orientations of a chemical shift tensor relative to a reference frame, together with the Euler angles that should be used with WSolids to represent this orientation. The second and third column of images shows the corresponding orientations for Simpson and lists the Euler angles that should be used with Simpson to represent these orientations.
| WSolids | Simpson (δzz = δ33) | Simpson (δzz = δ11) | |||
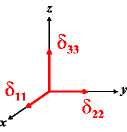 |
α = 0 |
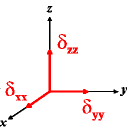 |
α = 0 |
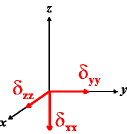 |
α = 0 |
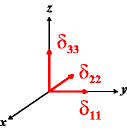 |
α = 90 |
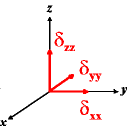 |
α = 0 |
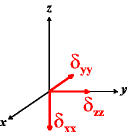 |
α = 0 |
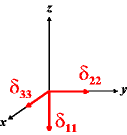 |
α = 0 |
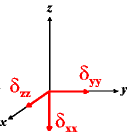 |
α = 0 |
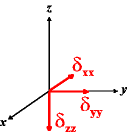 |
α = 0 |
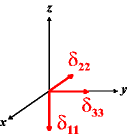 |
α = 90 |
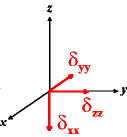 |
α = 0 |
 |
α = 0 |
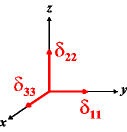 |
α = 0 |
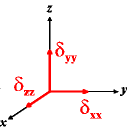 |
α = -90 |
 |
α = -90 |
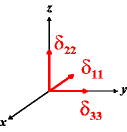 |
α = 90 |
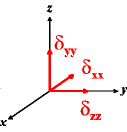 |
α = -90 |
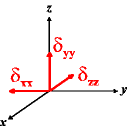 |
α = -90 |
References
| [1] | P. P. Man, Quadrupolar Interactions, In Encyclopedia of Nuclear Magnetic Resonance; D. M. Grant, R. K. Harris, Eds.; John Wiley & Sons, Chichester, UK, 1996, pp 3838-3848. |
[ Anorg. Chemie ] | [ Go Home ] | webm@ster | last modified: 20.03.2020

