Two-Dimensional Rotations

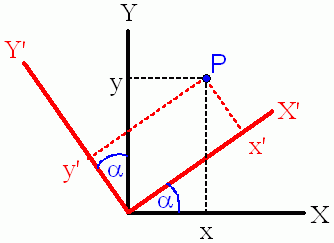Suppose the coordinates, (x,y), of a point in the two-dimensional XY system are known, but we are actually interested in knowing the coordinates of this point in another coordinate system, X'Y', which is related to the XY system by a counter-clockwise rotation by an angle α.

As the figure indicates, the coordinates of the given point in the new coordinate system will be:

   x' = x cos α + y sin α

   y' = -x sin α + y cos α

These transformations are explained in the next two pictures.

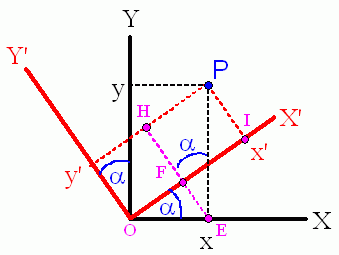Obtaining the new x' coordinate:

The old x coordinate of P corresponds to the length of the line between points O and E on the old X axis, |OE|. Similarly, the new x' coordinate of P corresponds to the length of the line between points O and I on the new X' axis, |OI|; we can see that this length is the sum of |OF| and |FI|. How does this help?
 
The projection of |OE| onto the new X' axis gives |OF|. Because the angle between X and X' is α and the angle between EF and OF is the right angle, it follows that:
|OF| = |OE| * cos α = x * cos α
 
Now let's look at another triangle: E H P
|EP| simply corresponds to the old y coordinate;
the angle between EP and EH corresponds to the rotation angle α and the angle between EH and HP is the right angle.
From this it follows that |HP| is given by:
|HP| = |EP| * sin α = y * sin α
 
Looking at the picture we can see that |HP| = |FI|, so that now:
x' = |OF| + |FI| = x * cos α + y * sin α

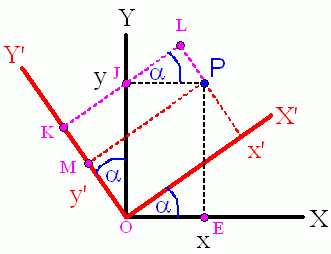Obtaining the new y' coordinate:

It works for the y' coordinate analogously:
We project the old y coordinate, |OJ|, onto the new Y' axis, |OK|. For the triangle O J K we can formulate:
|OK| = |OJ| * cos α = y * cos α
 
Now let's look at the triangle J P L, where we can calculate:
|PL| = |JP| * sin α = x * sin α
 
The picture shows that |PL| = |MK|, so that:
y' = |OM| = |OK| - |MK| = y * cos α - x * sin α